多重ループ: Sample 1: 共通項をループの外に(C)
■ 概要
ここでは式(1)にしたがって配列rとθから2次元配列xの値を計算します。2次元配列だから、2重ループを使用して配列xを求めます。
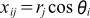... 式(1)
Code 1では式(1)を素直にコーディングしたものです。メイン計算では2つのループ、ループiとループj、を設けてその中に式(1)の右辺をそのまま計算しています。
Code 1のメイン計算をよく観察すると、cos(theta[i])はループjの中で不変であることが解かります。ループjの中でcos(theta[i])が不変なのに、N回も繰り返し計算されることになります。cosの計算は重い計算のなので、できるだけ減らしたいものです。Code 1は無駄に重い計算を繰り返しているので、非常に遅いプログラムになります。
Code 1を改良したのはCode 2です。ループjの中で計算されていたcos(theta[i])を、ループjの外に出して、一時変数dに記憶しておきます。その後ループjの中でこの一時変数dを使えば、Code 1とまったく同じ結果が得られるはず。違いはcos(theta[i])を1回で済むので、Code 1よりCode 2の方がはるかに高速に計算できるはずです。
ここで用いた高速化手法は実はダミー変数を使用の一種です。繰り返し使用されている値をダミー変数に入れておいて、その後はダミー変数の値を参照するから、その値の計算は1回にすることができます。
■ ソースコード
| ◆ Code 1 | ◆ Code 2 |
■ 計算時間の測定結果
Code 1とCode 2の計算時間の測定結果を表1に示します。ここではそれぞれのコードを5回実行して、平均とCode 1とCode 2との計算時間の比率も表示します。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | 平均 | 倍率 | |
|---|---|---|---|---|---|---|---|
| Code 1 | 4.32 | 4.31 | 4.46 | 4.31 | 4.29 | 4.34 | 9.59 |
| Code 2 | 0.42 | 0.45 | 0.47 | 0.45 | 0.47 | 0.45 | - |
■ 考察
Code 2はCode 1に比べて10倍弱速いという結果が得ました。配列のサイズNが大きければさらに倍率が大きくなるでしょう。
