多重ループ: Sample 2: ループの順番(C)

言語の変更： FORTRAN版

■ 概要

ここでは式(1)にしたがって配列rとθから2次元配列xの値を計算します。基本的にはSample 1と同じですが、違いはrとθのインデックスが入れ替わったことです。

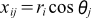... 式(1)

式(1)を素直にコーディングしたのはCode 1です。メイン計算では2つのループ、ループiとループj、を設けてその中に式(1)の右辺をそのまま計算しています。

θのインデックスが変わるものの、Sample 1と同様にcosの計算はN回で十分のはず。Code 1ではcosの計算がN×N=N²なので、改良する余地があります。しかしSample 1と違って、このサンプルではcos(theta[j])を単にループjの外に出すわけにはいきません。cos(theta[j])はループjの中では値が変化するからです。

ループの外に出すためにはその値がループの中で不変であることが条件です。Code 1ではcos(theta[j])の計算に一番近いループがjである以上、どうすることがありません。もしループiとループjを入れ替えられたら、直ちにcos(theta[j])をループの外に出せるようになります。そこで多重ループの順番の入れ替えが可能かどうかを検討します。今回のサンプルはループiとループjとの間に何もありませんので、ループの入れ替えはいうまでもなく可能です。

ループの入れ替え、そしてcos(theta[j])をループの外に出したのはCode 2です。このように書き換えれば、高速に計算でき、しかもCode 1とまったく同じ結果が得られます。

■ ソースコード

◆ Code 1

◆ Code 2

■ 計算時間の測定結果

Code 1とCode 2の計算時間の測定結果を表1に示します。ここではそれぞれのコードを5回実行して、平均とCode 1とCode 2との計算時間の比率も表示します。

表1 計算時間の測定結果(単位: sec)
	1回目	2回目	3回目	4回目	5回目	平均	倍率
Code 1	4.35	4.34	4.34	4.34	4.35	4.34	2.30
Code 2	1.87	1.89	1.89	1.89	1.90	1.89	-

■ 考察

Code 2はCode 1に比べて2.3倍速いという結果が得ました。しかしSample 1ほどの倍率はこのサンプルでは得られませんでした。このサンプルのCode 2がSample 1より遅い理由はメモリジャンプにあります(2次元配列を参照)。更なる高速化を達成したいなら、配列xの第1と第2のインデックスを入れ替えることも検討すべき。

前: Sample 1: 共通項をループの外に(C)

次: Sample 3: ダミー配列との併用(C)

多重ループ: Sample 2: ループの順番(C)